Warm-Up

On Predictions

Predict how much moxillation takes place at 70 traxolline.

Setting

Tidyverse

library("moderndive") #for get_regression_table()
library("tidyverse")

df_raw <- readr::read_csv("air_quality_demo_data.csv")

# brand colors
# orange on white: #e77500
# orange on black: #f58025

Data

This data set can be seen at aqicn.org and was accessed through the PurpleAir API

head(df_raw)

# A tibble: 6 × 6
  time_stamp          humidity temperature pressure pm1.0_atm pm2.5_atm
  <dttm>                 <dbl>       <dbl>    <dbl>     <dbl>     <dbl>
1 2023-06-10 06:00:00     34.3        81.3    1004.     0.355      0.64
2 2023-06-10 12:00:00     30.8        85.0    1003.     8.78      12.6 
3 2023-06-10 18:00:00     26.9        88.6    1003.    18.2       26.7 
4 2023-06-11 00:00:00     37.0        82.0    1005.    19.2       28.9 
5 2023-06-11 06:00:00     49.7        73.6    1006.    27.9       43.0 
6 2023-06-11 12:00:00     33.6        89.5    1006.    27.7       41.7

about 10 weeks of weather data, at 6-hour intervals (\(n = 291\) observations)
query: Why do we record different types of particulate matter measurements?

Wrangling

df <- df_raw |>
  separate(time_stamp, into = c("date", "time"), 
           remove = FALSE, sep = " ") |>
  mutate(time = ifelse(is.na(time), "00:00:00", time),
         day_part = case_when(
           time == "06:00:00" ~ "morning",
           time == "12:00:00" ~ "noon",
           time == "18:00:00" ~ "evening",
           .default = "midnight"
         )) |>
  rename(pm1_0 = pm1.0_atm, pm2_5 = pm2.5_atm) |>
  select(time, day_part, humidity, temperature, pm2_5)

separate the time stamp into date and time columns
described parts of the day: morning, noon, evening, midnight
renamed particulate matter columns for ease

head(df)

# A tibble: 6 × 5
  time     day_part humidity temperature pm2_5
  <chr>    <chr>       <dbl>       <dbl> <dbl>
1 06:00:00 morning      34.3        81.3  0.64
2 12:00:00 noon         30.8        85.0 12.6 
3 18:00:00 evening      26.9        88.6 26.7 
4 00:00:00 midnight     37.0        82.0 28.9 
5 06:00:00 morning      49.7        73.6 43.0 
6 12:00:00 noon         33.6        89.5 41.7

Linear Regression

response variable (\(Y\)): particulate matter (2.5 microns)
predictor variable (\(X_{1}\)): temperature

\[Y = a + b_{1}X_{1}\]

context: levels above 35 micrograms per cubic meter are considered unhealthy (according to the Indoor Air Hygiene Institute)

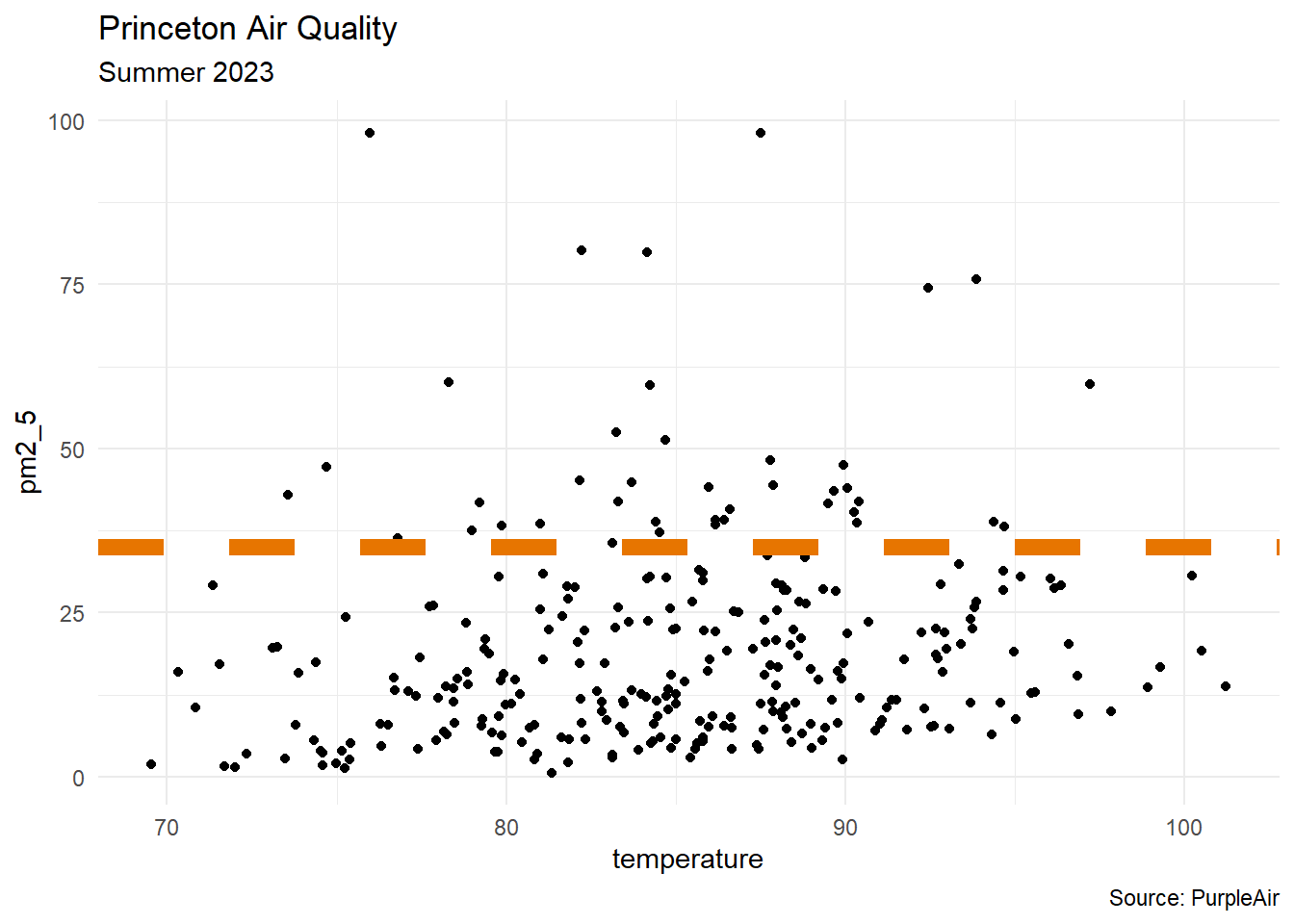
df |>
  ggplot(aes(x = temperature, y = pm2_5)) +
  geom_point() +
  geom_hline(yintercept = 35, color = "#e77500",
             linewidth = 3, linetype = 2) +
  labs(title = "Princeton Air Quality",
       subtitle = "Summer 2023",
       caption = "Source: PurpleAir") +
  theme_minimal()

Where Fit?

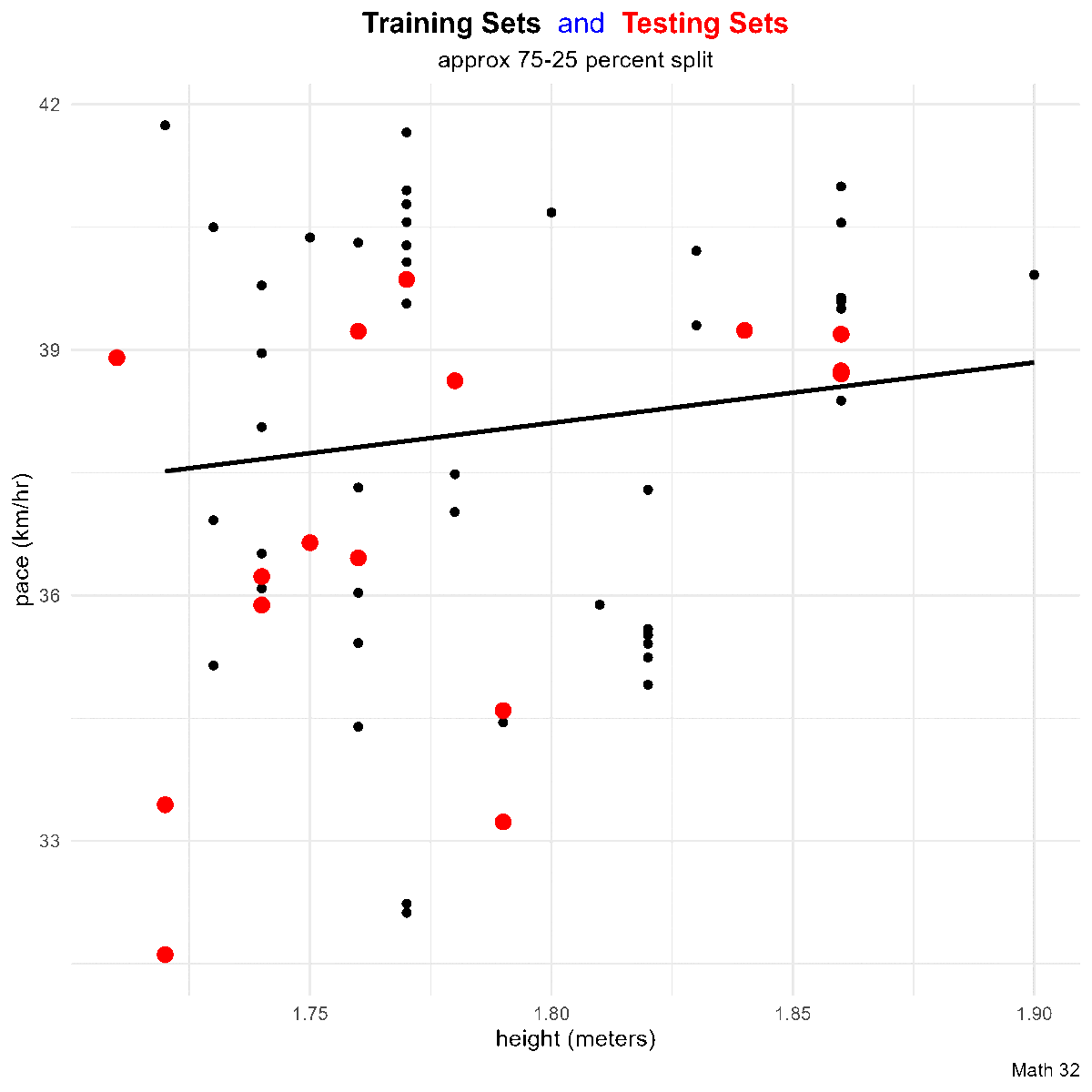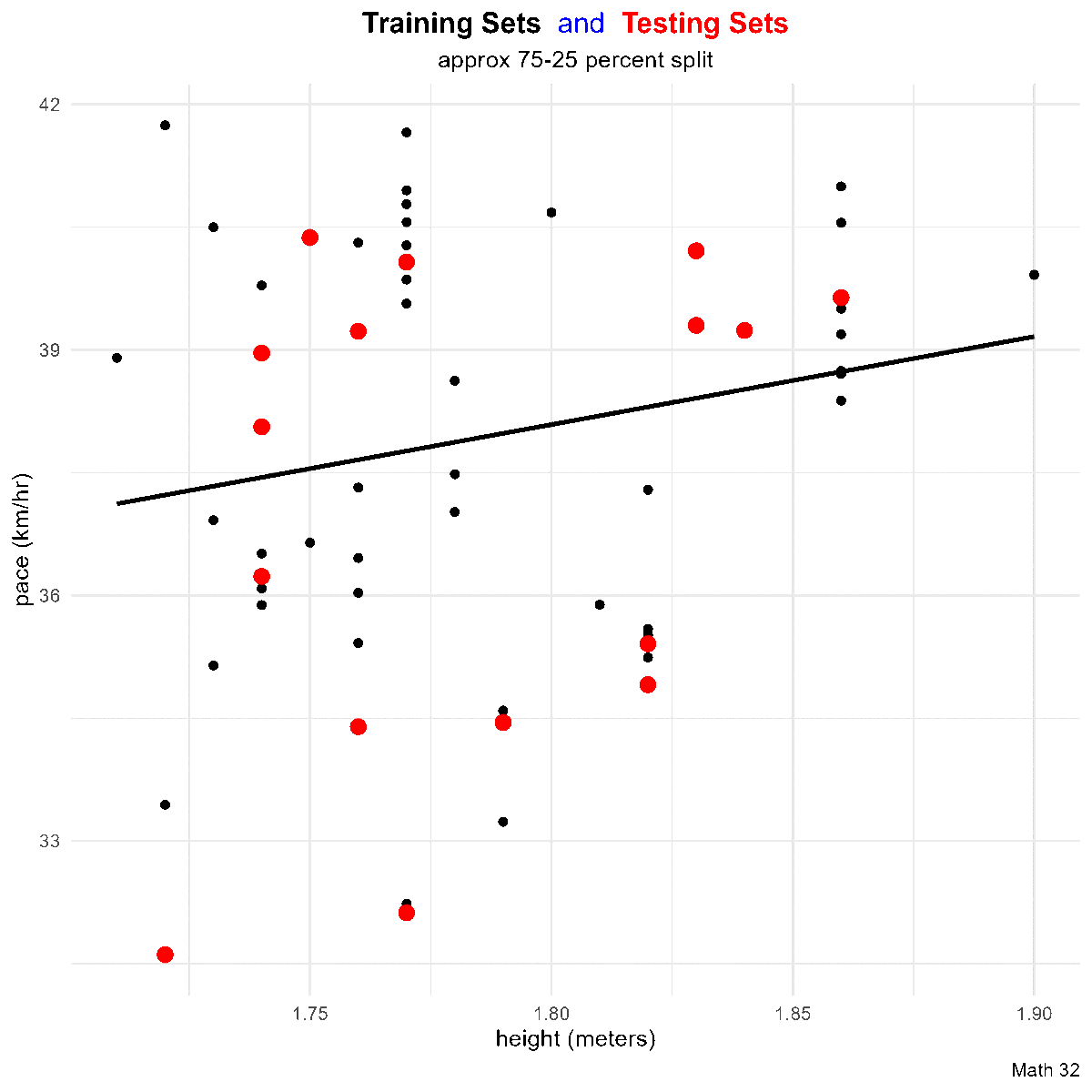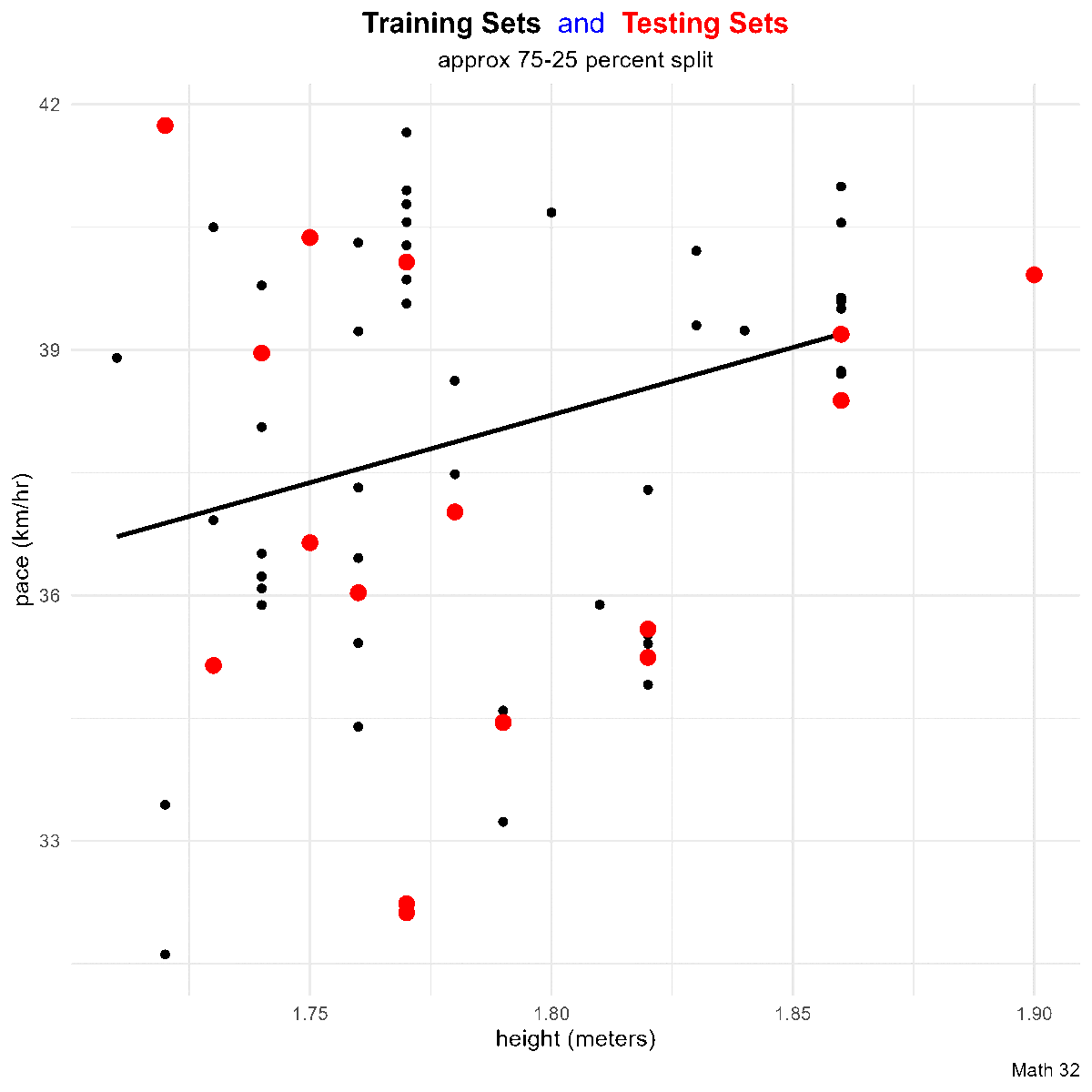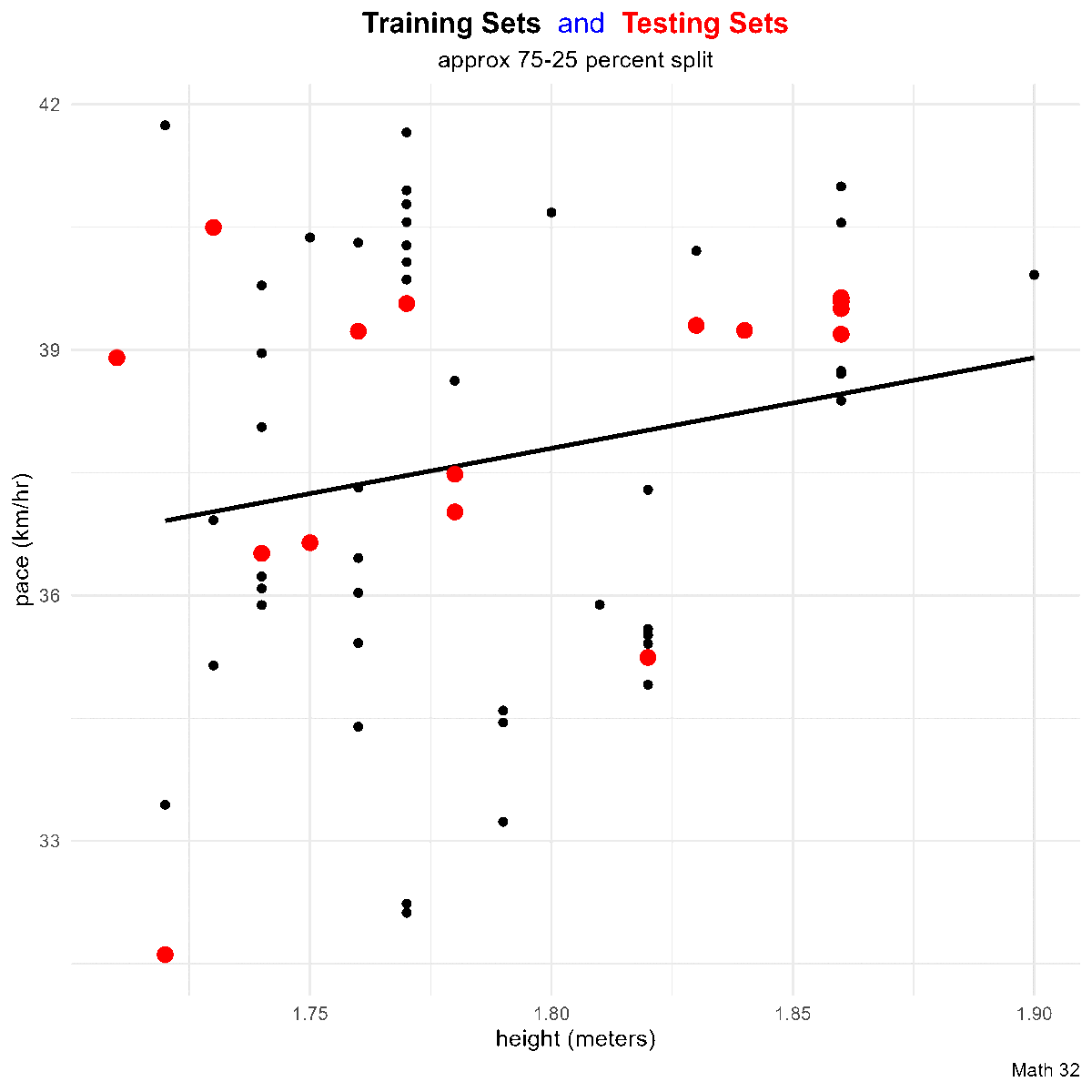
Residuals

Goal: Given a bivariate data set \(\{x_{i}, y_{i}\}_{i=1}^{n}\), form a linear regression model

\[\hat{y} = a + bx\]

that ``best fits’’ the data. Note that such a line will not go through all of the data (except in linear, deterministic situations), so

denote \(y_{i}\) for true outcomes
denote \(\hat{y}_{i}\) for estimates (or predictions)
then \(y_{i} - \hat{y}_{i}\) is the \(i^{\text{th}}\) residual

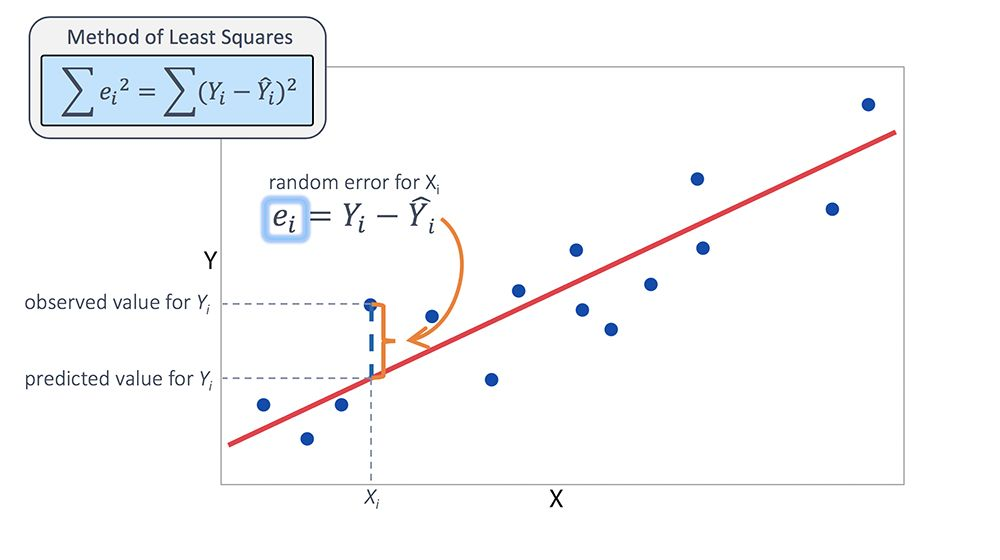
Method of Least Squares

Like our derivation of formulas for variance and standard deviation, scientists decided to square the residuals (focus on size of residuals, avoid positive versus negative signs). Let the total error be

\[E(a,b) = \displaystyle\sum_{i = 1}^{n} (y_{i} - \hat{y}_{i})^{2} = \displaystyle\sum_{i = 1}^{n} (y_{i} - a - bx_{i})^{2} \]

The ``best-fit line’’ minimizes the error.
To minimize the error, start by setting the partial derivatives equal to zero:

\[\displaystyle\frac{\partial E}{\partial a} = 0, \quad \displaystyle\frac{\partial E}{\partial b} = 0\] Thankfully, the function \(E(a,b)\) is an elliptical paraboloid, so there is a global minimum at the critical point, and that minimum is found where

\[a = \displaystyle\frac{ (\sum y_{i})(\sum x_{i}^{2}) - (\sum x_{i})(\sum x_{i}y_{i}) }{ n\sum x_{i}^{2} - (\sum x_{i})^{2} }, \quad b = \displaystyle\frac{ n\sum x_{i}y_{i} - (\sum x_{i})(\sum y_{i}) }{ n\sum x_{i}^{2} - (\sum x_{i})^{2} }\]

Linear Regression Model (Another View)

If sample means \(\bar{x}\) and \(\bar{y}\), sample standard deviations \(s_{x}\) and \(s_{y}\), and correlation coefficient \(r\) were previously computed, then the best-fit linear regression line \(\hat{y} = mx + b\) is computed with

\[m = \displaystyle\frac{ rs_{y} }{ s_{x} }, \quad b = \bar{y} - m\bar{x}\]

If correlation \(r > 0\), then the slope of the regression line is also positive
If correlation \(r < 0\), then the slope of the regression line is also negative

Outliers

In a scatterplot, an outlier is a point lying far away from the other data points. Paired sample data may include one or more influential points, which are points that strongly affect the graph of the regression line.

ggplot

The geom_smooth layer is a quick way to draw the linear regression graph in ggplot.

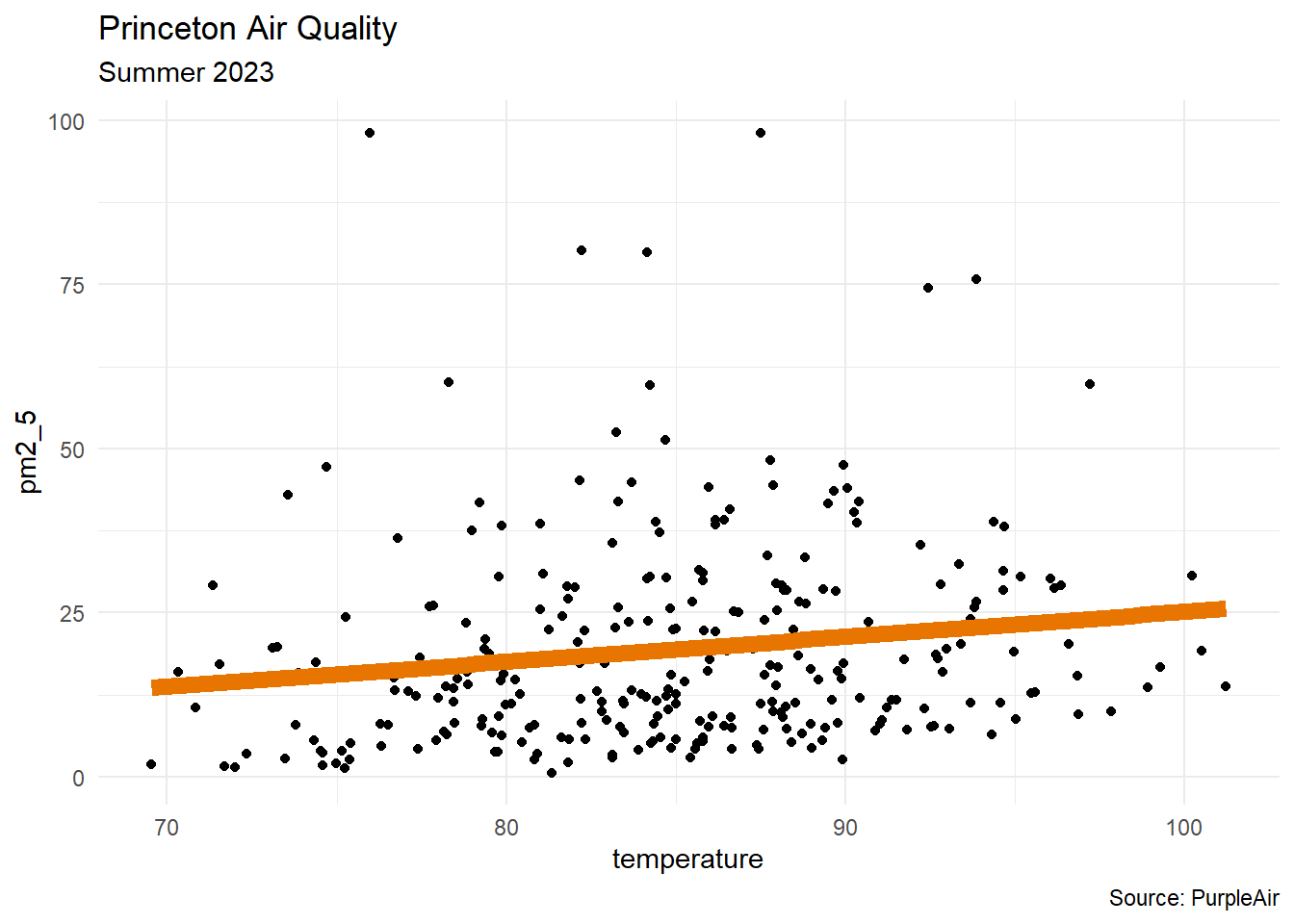
df |>
  ggplot(aes(x = temperature, y = pm2_5)) +
  geom_point() +
  geom_smooth(method = "lm", color = "#e77500", 
              linewidth = 3, se = FALSE) +
  labs(title = "Princeton Air Quality",
       subtitle = "Summer 2023",
       caption = "Source: PurpleAir") +
  theme_minimal()

Model

model1 <- lm(pm2_5 ~ temperature, data = df)

model1


Call:
lm(formula = pm2_5 ~ temperature, data = df)

Coefficients:
(Intercept)  temperature  
   -12.9066       0.3805

Interpretation: for every one-degree increase in temperature, the PM2.5 level increases by 0.3805

Prediction

Predict the PM2.5 level for a 78-degree day.

predict(model1,
        newdata = data.frame(temperature = 78))

       1 
16.77266

Think about what is meant by linear regression. Draw a large area for a graph (\(x\)- and \(y\)-axes, first quadrant only, you do not have to label the axes). Come up with a scatterplot situation where performing linear regression and a subsequent prediction would be a bad idea.

Multivariate Linear Regression

response variable (\(Y\)): particulate matter (2.5 microns)
predictor variables
- \(X_{1}\): temperature
- \(X_{2}\): humidity

\[Y = a + b_{1}X_{1} + b_{2}X_{2}\]

model2 <- lm(pm2_5 ~ temperature + humidity,
             data = df)

Describe the regression coefficients for the two predictor variables (hint: rates of change).

moderndive::get_regression_table(model2)

# A tibble: 3 × 7
  term        estimate std_error statistic p_value lower_ci upper_ci
  <chr>          <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
1 intercept    -10.8      15.7      -0.684   0.495  -41.8     20.2  
2 temperature    0.367     0.156     2.35    0.019    0.06     0.674
3 humidity      -0.02      0.093    -0.214   0.831   -0.203    0.163

Predict the PM2.5 level for a 78-degree day where the humidity is 50 percent.

predict(model2,
        newdata = data.frame(temperature = 78,
                             humidity = 50))

       1 
16.86311

Categorical Variables

response variable (\(Y\)): particulate matter (2.5 microns)
predictor variables
- \(X_{1}\): temperature

\[Y = a + b_{1}X_{1} + b_{3}X_{3} + b_{4}X_{4} + b_{5}X_{5}\]

\[X_{3} = \begin{cases} 1 & \text{morning} \\ 0 & \text{otherwise} \end{cases}\]

\[X_{4} = \begin{cases} 1 & \text{afternoon} \\ 0 & \text{otherwise} \end{cases}\]

\[X_{5} = \begin{cases} 1 & \text{evening} \\ 0 & \text{otherwise} \end{cases}\]

model3 <- lm(pm2_5 ~ temperature + day_part,
             data = df)

moderndive::get_regression_table(model3)

# A tibble: 5 × 7
  term               estimate std_error statistic p_value lower_ci upper_ci
  <chr>                 <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
1 intercept            -42.8     16.8       -2.54   0.012  -76.0      -9.68
2 temperature            0.68     0.184      3.69   0        0.317     1.04
3 day_part: midnight     5.06     2.89       1.75   0.081   -0.628    10.7 
4 day_part: morning      8.48     3.29       2.57   0.011    2.00     15.0 
5 day_part: noon         4.19     2.68       1.56   0.12    -1.10      9.47

Predict the PM2.5 level for a 60-degree morning.
Predict the PM2.5 level for a 75-degree evening.

\[Y = -42.844 + 0.680X_{1} + 5.056X_{3} + 8.477X_{4} + 4.186X_{5}\]

\[X_{3} = \begin{cases} 1 & \text{morning} \\ 0 & \text{otherwise} \end{cases}\]

\[X_{4} = \begin{cases} 1 & \text{afternoon} \\ 0 & \text{otherwise} \end{cases}\]

\[X_{5} = \begin{cases} 1 & \text{evening} \\ 0 & \text{otherwise} \end{cases}\]

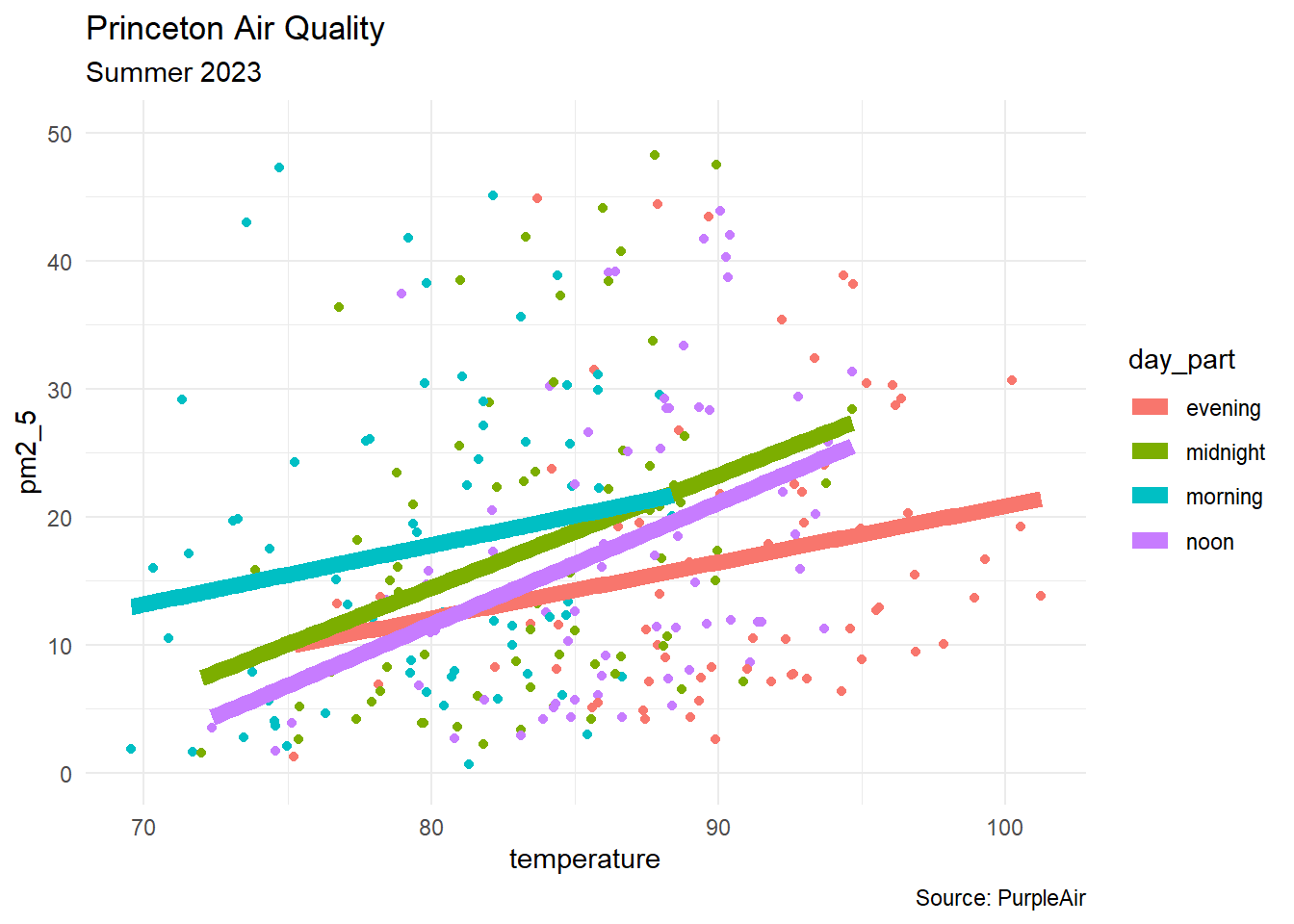
df |>
  group_by(day_part) |>
  ggplot(aes(x = temperature, y = pm2_5,
             color = day_part, group = day_part)) +
  geom_point() +
  geom_smooth(aes(color = day_part), method = "lm",
              linewidth = 3, se = FALSE) +
  labs(title = "Princeton Air Quality",
       subtitle = "Summer 2023",
       caption = "Source: PurpleAir") +
  theme_minimal() +
  ylim(0,50)

predict(model3,
        newdata = data.frame(temperature = 60,
                             day_part = "morning"))

       1 
6.448983

predict(model3,
        newdata = data.frame(temperature = 75,
                             day_part = "evening"))

       1 
8.176292

Looking Ahead

To Consider

How do we know that the predictions are reliable?
How do we know which model to choose?
How do we know which variables to use?

More Metrics

get_regression_table(model3)

# A tibble: 5 × 7
  term               estimate std_error statistic p_value lower_ci upper_ci
  <chr>                 <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
1 intercept            -42.8     16.8       -2.54   0.012  -76.0      -9.68
2 temperature            0.68     0.184      3.69   0        0.317     1.04
3 day_part: midnight     5.06     2.89       1.75   0.081   -0.628    10.7 
4 day_part: morning      8.48     3.29       2.57   0.011    2.00     15.0 
5 day_part: noon         4.19     2.68       1.56   0.12    -1.10      9.47

get_regression_summaries(model3)

# A tibble: 1 × 9
  r_squared adj_r_squared   mse  rmse sigma statistic p_value    df  nobs
      <dbl>         <dbl> <dbl> <dbl> <dbl>     <dbl>   <dbl> <dbl> <dbl>
1     0.046         0.033  235.  15.3  15.5      3.47   0.009     4   291

Book

Thanks!

Derek Sollberger
Lecturer of Data Science