Bayesian Neural Networks

Author

Derek Sollberger

Published

March 17, 2024

Over the next few weeks, I want to learn more about Bayesian Neural Networks. Here in this blog post, I will gather resources and examples.

Causal Impact

I have seen several people mention (on Twitter or Slack) the CausalImpact package. Here, I roughly follow the vignette.

library("CausalImpact")
library("tidyverse")

Toy Data

set.seed(320)

# create time series and apply vertical shift
ts_raw <- 100 + arima.sim(model = list(ar = 0.999), n = 100)

# add "noise"
y <- 1.2*ts_raw + rnorm(100) 

# intentionlly "break" time series and lift a part
y[71:100] <- y[71:100] + 25

x <- 1:100
df <- data.frame(x,y)
df |>
  ggplot(aes(x,y)) +
  geom_vline(xintercept = 70, color = "gray50", 
             linetype = 2, linewidth = 3) +
  geom_line(color = "red", linewidth = 2) +
  labs(title = "Time Series",
       subtitle = "with an induced discontinuity") +
  theme_minimal()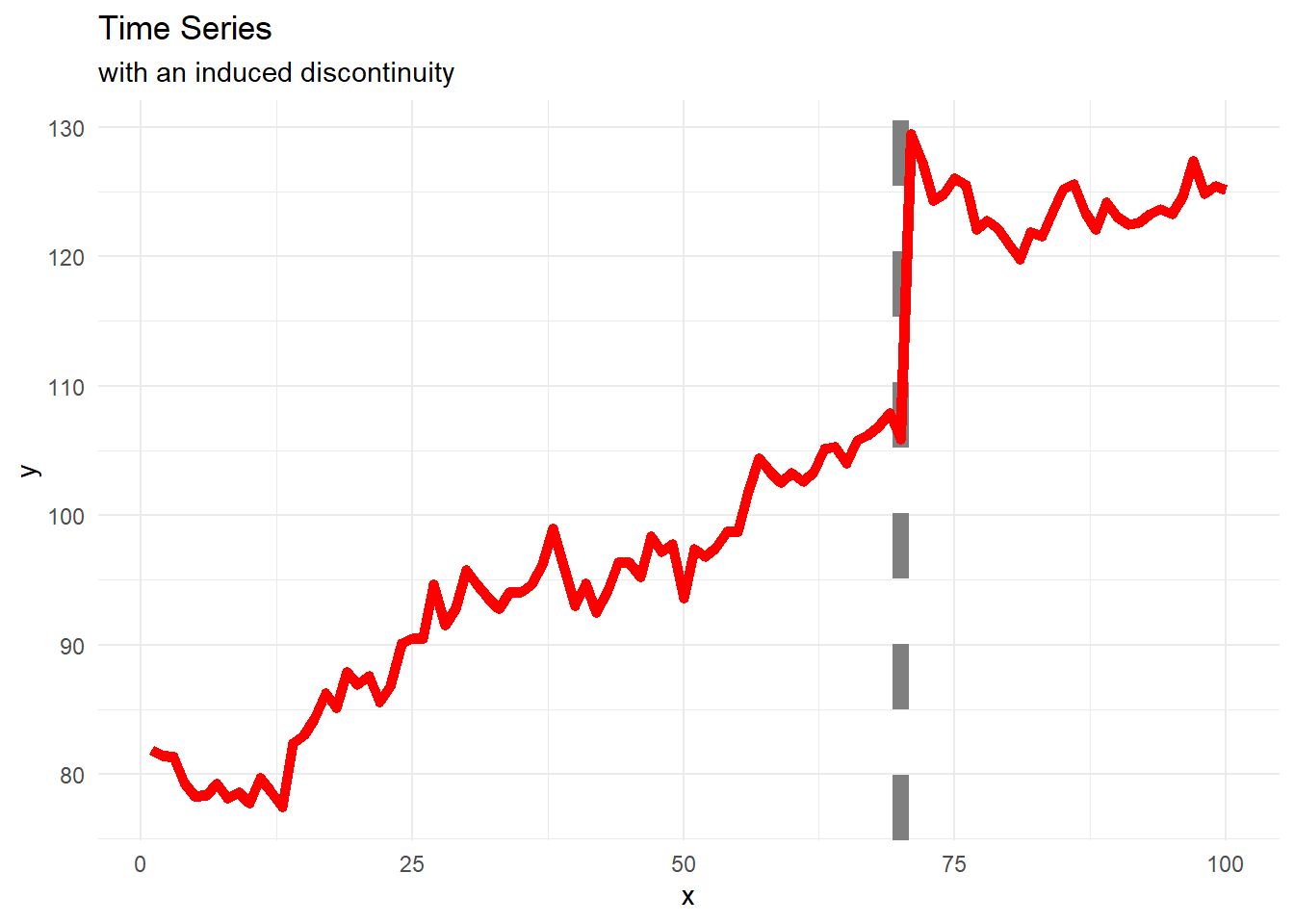

Bayesian Analysis

  • training over pre-intervention period

  • testing over post-intervention period

  • the CausalImpact function

    • assembles structural time-series model
    • performs posterior inference
    • computes estimates for casual effect
pre_intervention  <- c(1,70)
post_intervention <- c(71, 100)
ts_impact <- CausalImpact::CausalImpact(df,
                                        pre_intervention,
                                        post_intervention)

Model Statistics

summary(ts_impact)
Posterior inference {CausalImpact}

                         Average        Cumulative  
Actual                   86             2565        
Prediction (s.d.)        103 (3.8)      3100 (115.3)
95% CI                   [96, 111]      [2882, 3326]
                                                    
Absolute effect (s.d.)   -18 (3.8)      -535 (115.3)
95% CI                   [-25, -11]     [-761, -317]
                                                    
Relative effect (s.d.)   -17% (3.1%)    -17% (3.1%) 
95% CI                   [-23%, -11%]   [-23%, -11%]

Posterior tail-area probability p:   0.00106
Posterior prob. of a causal effect:  99.89418%

For more details, type: summary(impact, "report")

Visualization

The plot of an “impact” object returns a ggplot object!

plot(ts_impact)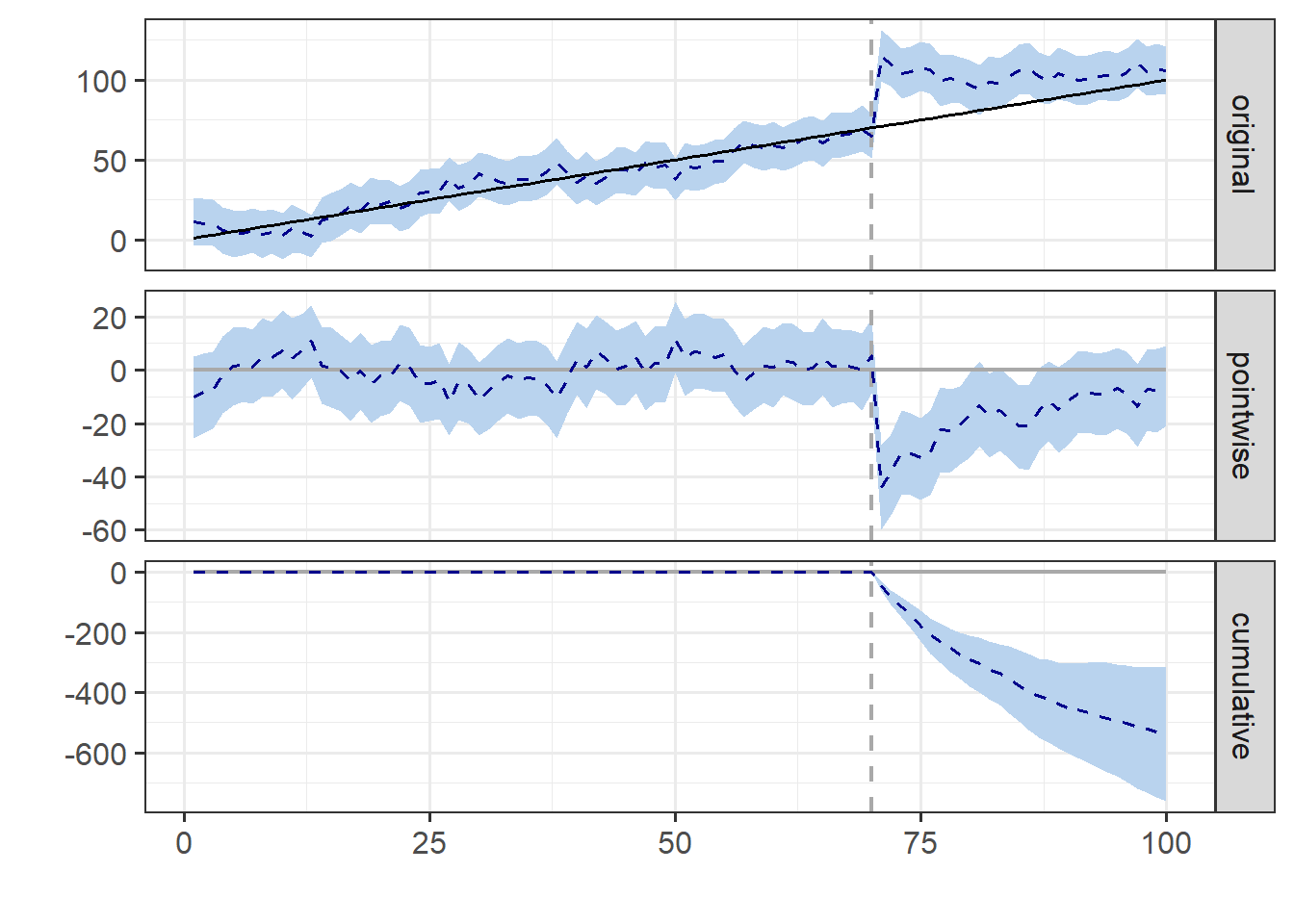

bsts

Bayesian structural time series

library("bsts")
data(iclaims) #unemployment data

Trend and Seasonal Components

state_specs <- 
  bsts::AddSemilocalLinearTrend(list(),
                                initial.claims$iclaimsNSA)
state_specs <- bsts::AddSeasonal(state_specs,
                                 initial.claims$iclaimsNSA,
                                 nseasons = 52)

Model

model_1 <- bsts::bsts(initial.claims$iclaimsNSA,
                      state.specification = state_specs,
                      niter = 100)
=-=-=-=-= Iteration 0 Tue Mar 19 23:21:31 2024
 =-=-=-=-=
=-=-=-=-= Iteration 10 Tue Mar 19 23:21:31 2024
 =-=-=-=-=
=-=-=-=-= Iteration 20 Tue Mar 19 23:21:31 2024
 =-=-=-=-=
=-=-=-=-= Iteration 30 Tue Mar 19 23:21:32 2024
 =-=-=-=-=
=-=-=-=-= Iteration 40 Tue Mar 19 23:21:32 2024
 =-=-=-=-=
=-=-=-=-= Iteration 50 Tue Mar 19 23:21:32 2024
 =-=-=-=-=
=-=-=-=-= Iteration 60 Tue Mar 19 23:21:32 2024
 =-=-=-=-=
=-=-=-=-= Iteration 70 Tue Mar 19 23:21:33 2024
 =-=-=-=-=
=-=-=-=-= Iteration 80 Tue Mar 19 23:21:33 2024
 =-=-=-=-=
=-=-=-=-= Iteration 90 Tue Mar 19 23:21:33 2024
 =-=-=-=-=

Visualization

plot(model_1)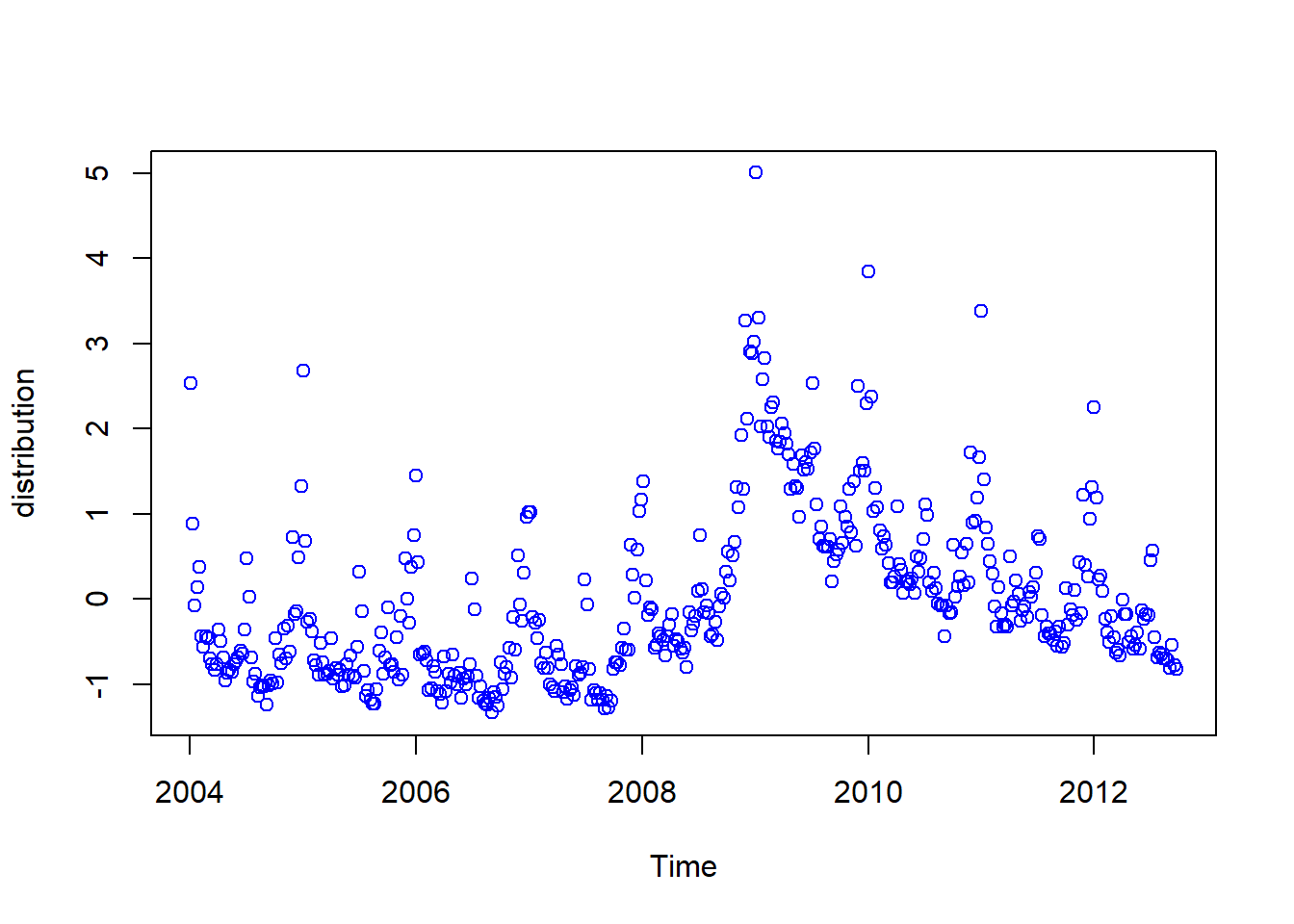

Prediction

  • predict next 12 time points
  • along last 156 time points (3 years)
pred_3y <- predict(model_1, horizon = 12)
plot(pred_3y, plot.original = 156)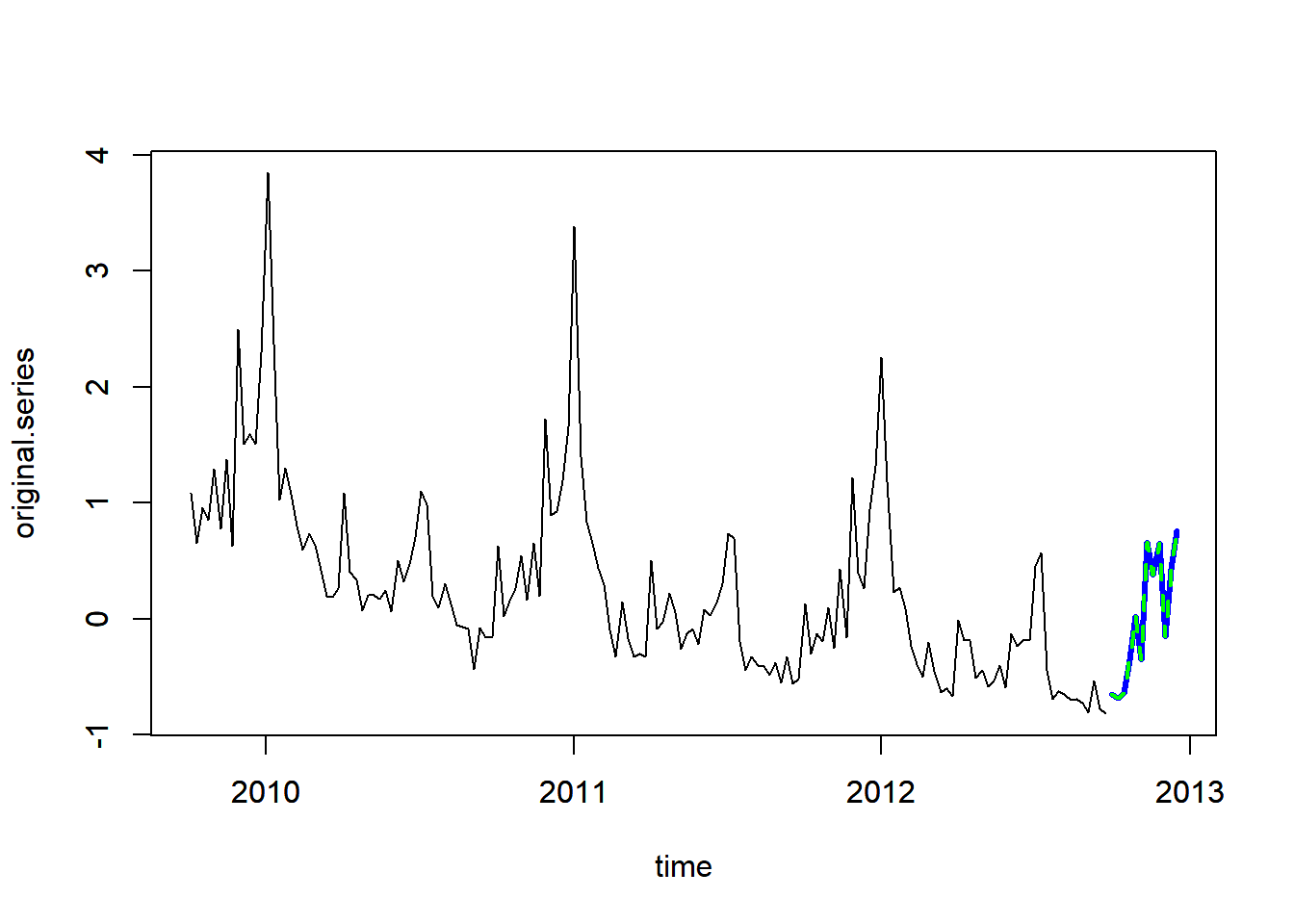

Online Videos